
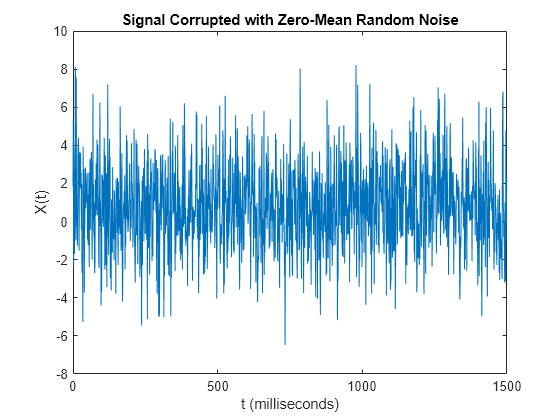
FFT is also used in physics and mathematics to solve partial differential equations (PDEs). Matlab, like most computational packages, implement a pretty neat set of fast Fourier transform algorithms referred to as FFTW: fastest Fourier transform in. In image processing, FFT is used for filtering and image compression. FFT is also sometimes used as an intermediate step for more complex signal processing techniques. Y fft( X ) computes the discrete Fourier transform (DFT) of X using a fast Fourier transform (FFT) algorithm. A FFT (Fast Fourier Transform) can be defined as the algorithm that can compute DFT (Discrete Fourier Transform) for a signal or a sequence, or compute IDFT (Inverse DFT). These techniques can be used for a variety of signals such as audio and speech, radar, communication, and other sensor data signals. Introduction to Matlab fft() Matlab method fft() carries out operation of finding Fast Fourier transform for any sequence or continuous signal.
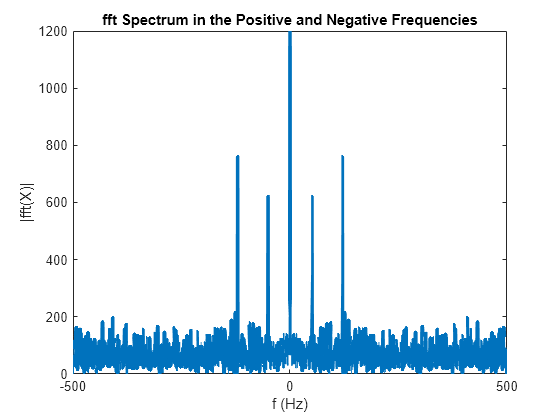
Variations of the FFT such as the short-time Fourier transform also allow for simultaneous analysis in time and frequency domains. In signal processing, FFT forms the basis of frequency domain analysis (spectral analysis) and is used for signal filtering, spectral estimation, data compression, and other applications. A straight computation of the DFT from the formulas above would take n2 complex multiplications and n(n 1) complex additions. FFT stands for Fast Fourier Transform, which is a family of algorithms for computing the DFT. The most commonly used FFT algorithm is the Cooley-Tukey algorithm, which reduces a large DFT into smaller DFTs to increase computation speed and reduce complexity. 1.2 Matlab: fft, ifft and fftshift To calculate the DFT of a function in Matlab, use the function fft. Popular FFT algorithms include the Cooley-Tukey algorithm, prime factor FFT algorithm, and Rader’s FFT algorithm.


 0 kommentar(er)
0 kommentar(er)
